Spinning Universe - How Spin and Gravity Orchestrate Order: Written on June 21, 2003
SPINNING UNIVERSE: HOW SPIN AND GRAVITY
ORCHESTRATE ORDER
- Abstract
- Introduction
- Materials and Methods
- Results
- Statistical Analysis
- Discussion
- Conclusion
- Acknowledgements
- References
- Tables
The orbits of the planets around the Sun and the satellites around the planets are along the ecliptic, and all are in the same direction as the mother bodies' axial spin. Further, these orbits have predictable velocity depending only on the distance from the central body; the above observations cannot be explained by mutual gravitation alone. Instead, the gravitational pull complemented by a rotational element from the mother bodies' axial spin will explain this effect adequately. This paper extends the above observations and in addition presents the crucial findings that through their own gravity and axial rotation, the gas giants actually control the direction as well as the speed of the axial rotation of the nearest, and synchronously rotating satellites.
As the combined effect of gravity and spin is to orchestrate an orderly motion of all bodies, it is proposed that they help maintain order in the solar system. Considering the fact that spinning is a universal finding, starting with the elementary particles and the nucleus of the atoms, the proto-stars and their planetary systems as well as the fully developed solar systems and the galaxies, one could conclude that this represents also a unifying system between matter at its smallest and the grandest. One could also logically deduce that the complementary relationship between spin and gravity does not end with the galaxies but the galaxies themselves orbit the center of the universe in one direction. Considering the grand scale of this spin, one could assess that the time scale for completion of one spin is of the order of billions of years. Some other ways in which the interaction of gravity and spin affect the structure and function of matter in the universe, including the generation and utilization of magnetism in planets will also be included in our discussion.
KEY WORDS:
Spin, orbit, axial rotation, gravity, solar system, galaxies
In 1929 Edwin Hubble observed increased red shift of light from distant galaxies and, the more distant the galaxies were, the more red shifted the light from those galaxies was (1). This was interpreted as a flight of all galaxies away from every other galaxy and matter in the universe and, by extrapolation, it was assumed that initially the universe itself was born in a gigantic explosion. This was dubbed the "Big Bang" and an arbitrary age of 13-15 billion years was proposed. When Penzias and Wilson discovered a uniform level of radiation in every direction (Cosmic Microwave Background Radiation or CMBR), it was proposed as the remnant of this initial explosion and confirming the Big Bang theory (2, 3). The scientists who followed Hubble proposed an initial "inflation" of the universe in the first 10 -30 seconds and a continuing expansion of the universe ever since (4-7). The currently accepted model of the universe is that space itself is being made at nearly the speed of light, from nothing, ever since the Big Bang. Many studies have been quoted as confirming this expansion of the universe, with accelerating flight of the more distant galaxies (8-13). Recently, this has even revived the notion of Einstein's "cosmological constant" as being responsible for this acceleration of the 'expansion' of the universe (14, 15).
The validity of the above assumptions can be questioned on at least two counts. First is our common observation of celestial bodies rotating on their own axes and orbiting the largest object in their vicinity. Since this axial rotation is also observed in matter at the smallest (such as the electrons) and the grandest (galaxies) levels, one could argue that the galaxies themselves must move in the space circumferentially (orbit), rather than in a radial direction, as was suggested by Hubble's observations. This author intuitively assumed that, since all the components that go into making galaxies exhibited this spin, galaxies themselves must obey the same rules. It is proposed that the increased red shift was simply this circumferential motion and for measuring movements of objects at such vast distances red shift of light was not satisfactory. One could also argue that, unless our earth was at the very center of the universe, we must observe some galaxies and stars moving towards us and thus be blue-shifted. One could be critical about the fact that what Penzias and Wilson observed was made only around the earth, an insignificant speck in the vast ocean of the universe. Then to extrapolate to the infinitely large void of space in the whole universe was not something one could subscribe to.
Once this author became convinced that if one extrapolated to the whole universe the observed property of matter from the smallest to the largest entities, those ideas were written down in a paper in the year 2000, entitled "Spinning Universe: A Hypothesis". However that paper was not published in print but in 2011 the paper was posted as the backbone of a website, along with some other articles in related topics in astronomy; the site is: www.spinninguniverse.com (16). A study published in Physics Letters by Michael Longo in May 2011 validated this idea (17). His study charted the axial rotation of 15,158 spiral galaxies with red-shifts of <0.085 and it showed that an excess of left-handed spiral galaxies or displaying axial rotation in a counter-clockwise direction when observed from the Northern Hemisphere. The clear inference was that, as opposed to the radial movement suggested by Hubble, the matter in the universe (represented by the galaxies' own spin direction) was 'spinning' in one direction. The current article is written with the specific purpose of explaining how the interaction of the spin of the bodies and the inherent mutual gravitational pull keeps order in the universe.
As the solar system can be considered a representative unit of the universe, with a complex system of bodies obeying roughly the same physics that perhaps obtains in all parts of the universe, the available data about that system was reviewed. This decision was also influenced by the fact that data are available in sufficient detail. Thus, the data dealing with the solar system, provided by NASA on their website (http://nssdc.gsfc.nasa.gov.html) were studied in depth. Close attention was paid to the rotational and orbital parameters and those other factors that might have a bearing on them. The distance from the Sun, the mass and size of the bodies, their intrinsic axial spin and orbital parameters and other properties such as magnetism were also examined in detail. Current astronomical literature referenced in this paper was also studied as it applied to the architectural and functional aspects of the universe.
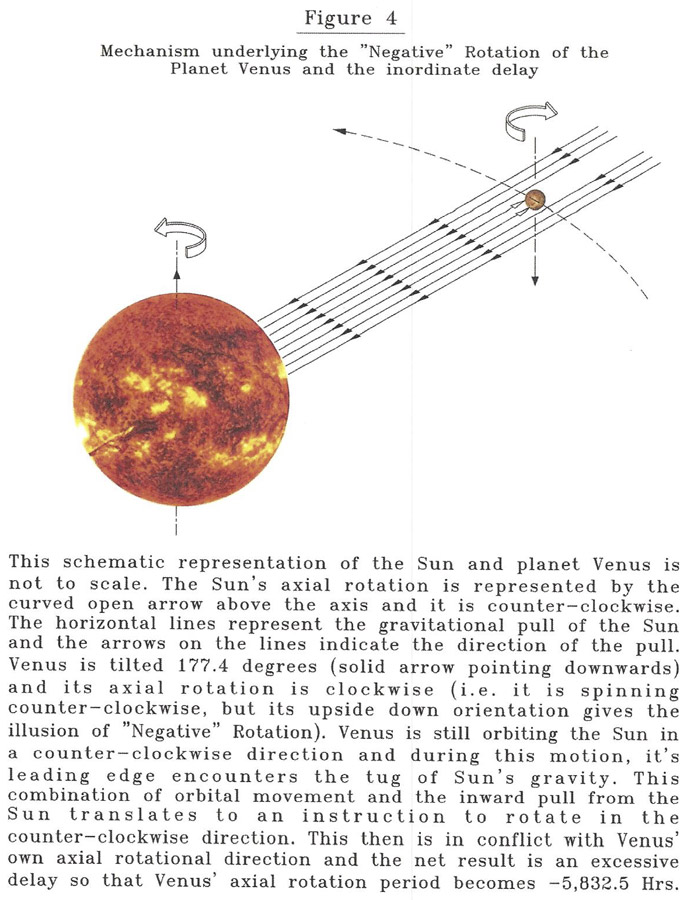
Table I presents the orbital parameters of all the planets of our solar system and some other salient features. Included in the analysis are the mass, diameter, density, distance from the Sun, orbital velocity, orbital period, aphelion, perihelion, gravity, axial tilt and rotation period. The distance from the Sun shows a direct relationship with the orbital velocity, as predicted by the inverse square law. Both perihelion and aphelion also increase with the distance from the Sun. One curious feature is the 'negative' axial rotation in Venus, Uranus and Pluto; both Venus and Pluto also display undue delay in the rotation period; explanation of this follows in the Discussion section.
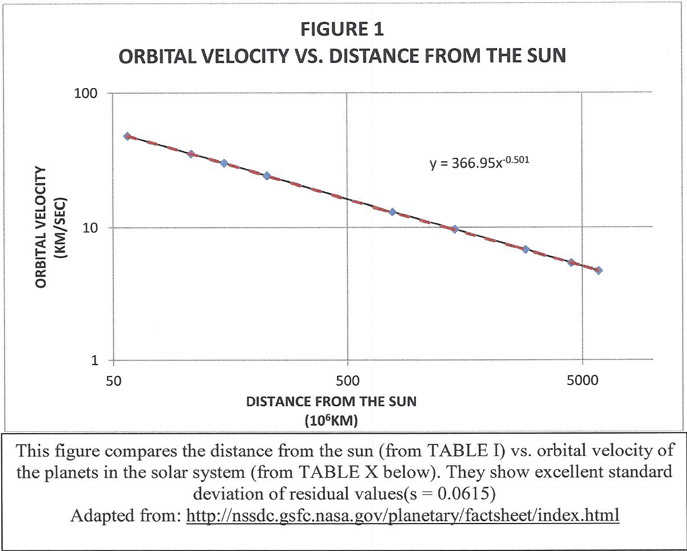
Fig. 1 compares the distance of the planets from the Sun and the orbital velocity and shows how closely they are related. It proves the veracity of the inverse square law.
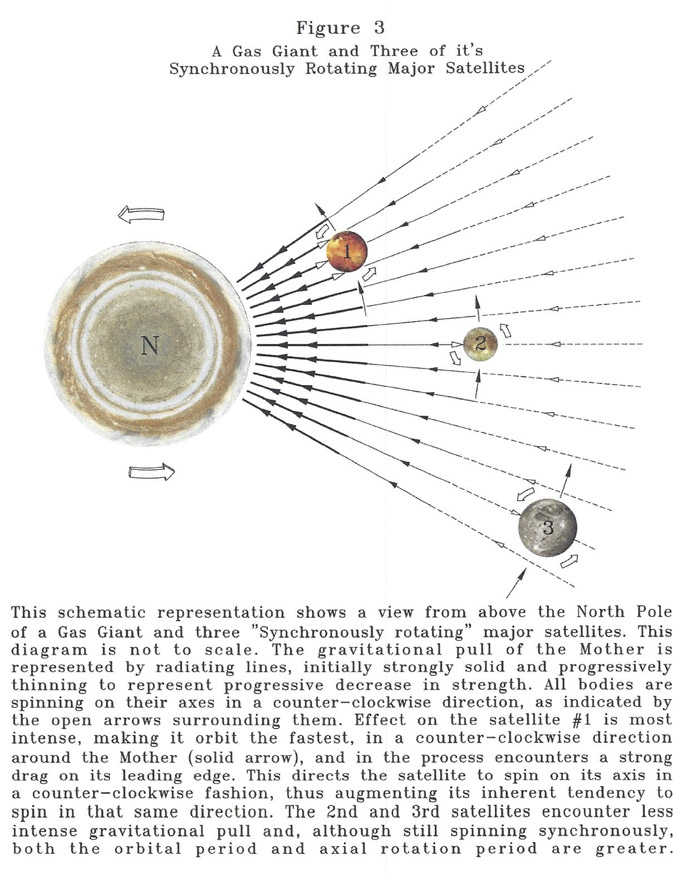
Table II presents the orbital parameters of Jupiter and its known satellites. Jupiter's was chosen as a prototypical planetary system but Saturn's and Uranus' systems follow a similar pattern but are not shown here for the sake of brevity (these were reported in ref #18). Neptune's details are incomplete at present. All of them confirm the accuracy of the inverse square law as it applies to these planets and their satellites as well. Two interesting findings in this table are the 'synchronicity' (Synchronous rotation, which means the axial rotation period and the orbital period are the same) of the large satellites that are closest to the gas giants and the 'reverse rotation' of the 'lesser' satellites that are far away. The synchronicity can be understood if one considers that the proximity to the mother allows the free and unhindered gravitational influence to be transmitted to the satellite. Further, not only does this mean the gravitational pull and the centrifugal force imparted by the spin of the mother to the satellite, induce it to orbit faster, closer it is to the mother, but also hints at the mother body's ability to actually spin the satellites faster on their axes, the closer the satellite is to the mother. As these satellites are continuing to spin on their axes, this is the only likely explanation for this interesting finding. The explanation for the second phenomenon ("reverse rotation", which means the axial rotation of these bodies is opposite to that of the mother planet) is less straight-forward. Since all of these satellites also exhibit large orbital inclination (it is unknown if this means also large tilts of their axes), one could deduce that, similar to the planets with axial tilts of over 90 degrees (Venus, Uranus and Pluto), the axial rotation is still anticlockwise but the upside down orientation of their North poles give the illusion of rotating in an opposite direction.
Table III lists the closest major satellites of the gas giants, Jupiter, Saturn and Uranus and earth's own moon. All of these orbit their respective mother planets in a synchronous manner (This means the axial rotation period and the orbital period are the same). The axial tilts of these satellites of the gas giants are not available for review but that of our moon is only 6.7 degrees. NASA's website does indicate that the orbital inclination of these bodies is less than 2 degrees, with only an odd satellite displaying orbital inclination higher but most of them are still below 15 degrees. It is not known if the axial tilts will parallel the orbital inclination. It is to be stressed that all are situated close to the mother body. Thus, a large gravitational influence from the mother body must have a major role in this phenomenon (synchronicity). This phenomenon is explored below and in the Discussion.
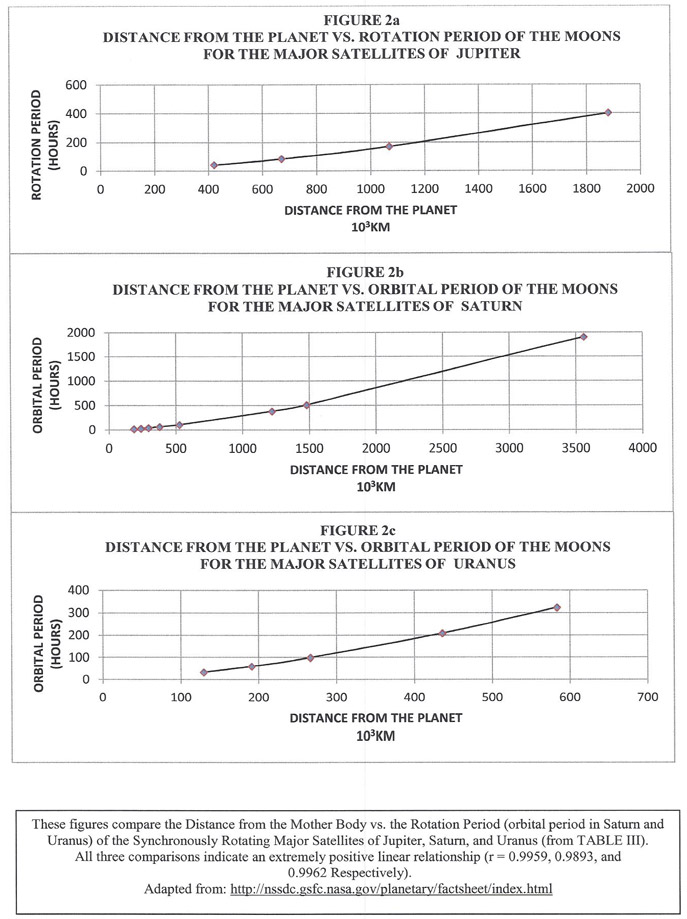
Fig 2 a-c: Shown in these three figures are the relationships between the distance of the major (also closest) satellites from their respective gas giant central bodies and the speed of their axial rotations. This finding has major implications in the phenomenon of synchronous rotation of these satellites, and bolsters the idea put forward in this paper that spin of the mother bodies have major impacts on the behavior of their satellites, besides the effect on the orbital velocity. The mother bodies actually augment the speed of axial rotation of the synchronously rotating satellites. The NASA's website did not provide similar details about the major (synchronously rotating) satellites of Neptune.
Table IV compares the planets with the most pronounced axial tilts (Venus, Uranus and Pluto) with two "typical" planets, the Earth and Jupiter. The former three planets have 'negative' rotation (axial rotation opposite to the Sun's) and, the solid planets (Venus and Pluto) also have considerable delay in the rotation period. A reasonable inference from these observations is that, the increased axial tilt makes these planets' axial rotation compete with the gravitational/rotational influences from the mother (Sun) and thus, a considerable delay in the axial rotation occurs. The reason for lack of delay of the axial spin of Uranus is unknown but one plausible explanation may be that since it is a gas giant, despite its increased axial tilt, the axial rotation is not slowed. Or, perhaps, for the axial rotation to slow down, the tilt may have to be much higher, quite possibly higher than 90 degrees.
The statistical analysis associated with this research stems from the special relationships between the Sun and its planets and between the gas giants and their major satellites. Pearson's correlation coefficient (r) was calculated and the results are given below:
Correlation between the Sun and the Planets
The data given in TABLE I represent several planetary facts on the planets in our solar system. In the first analysis, the correlation between the independent variable (X), distance from the sun was compared to the dependent variable (Y), orbital velocity of the planets and the correlation coefficient was calculated. The data values used for this calculation were taken from TABLE I and plotted in FIGURE 1.
TABLE Y indicates the correlation coefficient for the relationship between the independent variable, distance from the sun compared to the dependent variable, orbital velocity of the plants. The correlation coefficient of r = -0.76 was established. The correlation coefficient of r = -0.76 represents a moderate relationship that is neither strongly nor weakly related.
When the associated data values from TABLE I were taken into consideration, a simple Power Regression trend was calculated for the distance from the sun vs. the orbital velocity of the planets.
Using the trend function capabilities of EXCEL software, the following equation was determined to be a very strong fit for the data and well represents the Inverse Square Law.
When the independent variable, distance from the sun, was substituted in this equation in place of the variable X, the fitted values for Y were calculated. The standard deviation of residual values for this data set was established at s = 0.0615. This value represents an excellent fit based on the above power regression function for the data.
Correlation between the Planets and their Moons
In the second part of the statistical analysis, the correlation between the independent variable; distance from the mother were compared to the dependent variable, orbital period (or rotation period) and the correlation coefficients were calculated. The data values for the earth and three Gas Giants and their moons are shown in TABLE III and plotted in the associated FIGURES 2a - 2c.
When the data for the independent variable, orbital distance of the moons of the three Gas Giants, Jupiter, Saturn, and Uranus were compared to the dependent variable, orbital period and were subjected to the correlation calculations, the correlation value of r = 0.9959, 0.9893, and 0.9962 respectively was indicated in TABLE Y. As FIGURES 2a, 2b, and 2c show this is an extremely strong positive correlation and shows strong statistical support for the hypothesis that the variables of distance from the mother and rotation period (or orbital period) of the major satellites of these three Gas Giants are related.
|
COMPARISON |
CORR. |
|
DISTANCE FROM THE SUN VS. ORBITAL VELOCITY OF THE PLANETS |
-0.7600 |
|
DISTANCE FROM JUPITER VS. ORBITAL PERIOD OF THE MOONS |
0.9959 |
|
DISTANCE FROM SATURN VS. ORBITAL PERIOD OF THE MOONS |
0.9893 |
|
DISTANCE FROM URANUS VS. ORBITAL PERIOD OF THE MOONS |
0.9962 |
The major finding presented in this paper is the close relationship between spin (both the axial rotation and the orbital movement) and gravity. This finding bolsters the idea that spin and gravity work in tandem and their complementary relationship is crucial for the orderly movements of all celestial bodies. Considering the fact that spin, which is exhibited by all elementary particles as well as large bodies such as planets, stars and galaxies, and the fact that even the generation of charge requires spin, one could make the case for spin being the most important fundamental property in nature. Also, since spin is exhibited by fundamental building blocks as well as the largest entities in the universe, one could argue that it is the one unifying force between the infinitely small and the infinitely large.
DIMINISHING ORBITAL VELOCITY WITH DISTANCE FROM MOTHER BODIES:
The diminishing orbital velocity of the satellites depending on the distance from the mother body can only be explained by the inward pull of gravity being counter-balanced by an equal and opposite centrifugal force of some sort, emanating from the mother body. Newtonians ascribe this effect to obeying his 1st law of motion. However, how will this effect explain the direction of the orbits matching that of the mother body's axial spin, the orbital velocity diminishing depending only on the distance from the mother and all the satellites being situated around the ecliptic of the mother bodies? Einstein's "warping of the fabric" of "space-time" by the gravity of the celestial bodies will only help explain why other bodies might be situated where they are situated, but cannot explain why all bodies rotate on their own axes and orbit a larger neighbor at only around the ecliptic and with a diminishing orbital velocity, the farther away they are from the mother bodies.
DIMINISHING SPEED OF AXIAL ROTATION WITH DISTANCE FROM THE GAS GIANTS IN SYNCHRONOUSLY ROTATING SATELLITES:
Information in sufficient details on the satellites exhibiting synchronous rotation was available for the major satellites of Jupiter, Saturn and Uranus. These show clear evidence for a 'rotational influence' from the gas giants to these satellites. The diminishing speed of axial rotation of these satellites, depending only on the distance from the mother strongly suggests such an effect. The standard 'default' explanation in cosmological teaching, of 'tidal forces' cannot even begin to address this crucial finding. It is to be noted that, in non-synchronous rotation, which obtains in the pattern of axial rotation with non-synchronously rotating bodies, this effect may not apply; obviously, the distance alone might mean a much diminished effect from the mother. It is not known for what purpose this effect (augmenting the speed of rotation) that the mother body has on its nearest neighbors.
SATELLITES ORBIT CLOSE TO THE ECLIPTIC:
From the time of formation of the proto-stars, to the fully developed solar systems, and the satellite systems of the planets including the rings and ring systems, within the solar system, the lesser bodies align themselves close to the equatorial region (the "ecliptic"). In fact, one does not find satellites orbiting the mother bodies at random orbits, unlike the 'electron clouds' that scientists claim the orbits of the electrons around the nucleus are. One could suspect the electrons also take up an 'equatorial' location for maintaining their orbits as well. The vast majority of the galaxies are spiral or elliptical and their component stars are also situated around the equatorial location of the galaxies. Clearly, this arrangement seems to be fundamental and probably also participates in imparting order in the universe and its component systems. The question to be answered is how? If one applies the principles enunciated in this paper, one can conclude that there is enhanced gravity around the mid-portion of a planet, a star or a star system which we call galaxy and, it and the spin of the body will direct the orbits of the satellites to this location. This is yet another example of gravity and spin working together to impart order.
"SYNCHRONOUS" AND "REVERSE" ROTATION OF PLANETS AND SOME OF THEIR SATELLITES:
A scrutiny of the Tables will reveal a curious relationship between the axial tilts of the satellite bodies and the presence of 'synchronous' rotation, ordinary rotation or a 'reverse' rotation of the satellites. In the case of the planets, (Tables I and IV) the three that have axial tilts larger than 90 degrees display 'reverse' or 'negative' rotation; these are Venus, Uranus and Pluto. This phenomenon means the direction of the axial rotation of these bodies is counter to the direction of rotation of the parent and all the other bodies. The reverse is true for those bodies that have negligible tilts of their axes (less than 1 degree, Tables II & III); the closest large satellites of Jupiter, Saturn, Uranus and Neptune are examples. Those bodies that have axial tilts between these extremes have 'normal' axial rotation. The question is why? It is believed that the explanation lies in the effect the mother bodies have on their satellites' axial rotation itself by the spin, emanating from the dominant body. The explanation for the synchronous rotation is given in a prior paragraph and it clearly attests to this belief; the close relationship between the distance of the satellites from the mother and the speed of axial rotation of the satellites strongly supports this assumption. In the case of the 'reverse' rotation, since the axes of the bodies are tilted sufficiently, the net effect is that the mother bodies' influence, again through the combination of gravity and spin is opposite to that of the daughters'. Thus, a slowing of the satellite's axial rotation occurs, as well as a suggestion of rotation in the 'reverse' direction; it is as though the mother body is instructing the satellite to rotate in one direction but since the satellite's axis is tilted by so much, the satellite's own tendency competes with the mother's instruction and thus is slowed. As was stressed by this author in an article that is in press (Physics Essays, 26:2, June 2013, Ref# 18) this is a particularly telling phenomenon; it attests to the fundamental nature of the direction of rotation of the bodies. One could conclude that the normal axial rotation is anti-clockwise, relative to the North Pole, in all bodies and all systems.
Earth's only moon displays the same synchronous rotation as the closest satellites of the gas giants. Situated at 378,000 Km from the earth, the moon orbits in the same direction as the mother's axial rotation. Curiously, during all of its orbits, through the phases (which depend on the shadow cast by the earth during the moon's transit) an observer from the earth only sees one side of the moon. Now, how is that possible? Since the moon is also spinning on its own axis, while also orbiting the earth in a very close range, it behaves like the closer large moons of Jupiter, Saturn, Uranus and Neptune. The moon's axial rotation takes 27.322 earth days, while its orbital period is 27.3217 days. This is a very special relationship between the moon and the earth at present and it depends on the distance between the two bodies at this moment in time. As the moon is slowly moving away from the earth, this special relationship will change steadily. Solar eclipses will slowly change from being complete to one with a complete ring of sun showing around the moon, sometime in the future.
MAINTAINING ORDER IN THE UNIVERSE AND MAINTAINING THE SHAPES OF BODIES
This interplay of gravity and spin applies to the behavior of matter at the smallest, as well as that of the grandest. The effect on the matter at the grandest (planets, stars and galaxies) is to maintain their motion in space only in one direction, at specific velocities, both of which help obtain order in the universe; otherwise, if all bodies were to orbit at random the bodies will be constantly colliding with one another. There are several other phenomena in the universe that this combination can help explain. One is the shape that large bodies such as stars and planets assume. When such bodies form, the gravitational pull of matter that make up these bodies, compresses this matter from every direction and the bodies assume a roughly spherical shape. However, all these bodies are not totally spherical; they bulge somewhat around the equator, making the circumference around the equator more than that through the poles. This is due to the centrifugal force exerted on matter by the axial spin of the body itself. In fact, this effect is what counter-balances the incessant inward pull of gravity in stars, rather than the usual belief that the nuclear fusion is responsible. Otherwise, the shape assumed by stars might look more irregular. This idea is dramatically reinforced by the shape assumed by a star that rotates on its axis at extremely high speed (the star is "VFTS 102" nick-named "Burger Star", (19) which is located 160,000 light years away, in the Large Magellanic Cloud, a satellite galaxy of Milky Way Galaxy. It rotates on its axis at 1 million miles per hour!). Also, it will be hard for one to explain how those bodies that do not ignite, the planets and their satellites, also attain roughly the same shape as that of the stars.
GENERATION OF MAGNETISM IN SPINNING BODIES
The explanations offered by scientists for the generation of this property are numerous, confusing and inconclusive. Most authorities attribute the generation of magnetism in planets to some form of "magneto-hydrodynamic dynamo" (20). The most widely accepted version of this is "a dynamo action in a geomagnetic field, made by convection motions in the earth's electrically conductive field made by convection motion in the earth's electrically conductive fluid core" (21). A problem with this explanation is that such magnetism cannot co-exist with the intense heat that exists in the molten iron core (22). A nuclear fission-driven 'geo-reactor' which leads to heat production and thereby convection has been proposed as an alternative explanation (23). None of the explanations is conclusive and all are open to criticism. If one uses the findings given in this paper, one could explain the generation of the electromagnetism this way: Central to this idea is the molten iron in the core, which is a function of the gravitational push towards the center of the globe. Since the earth rotates on its own axis (at the relatively fast pace of 1,675 Km/H), all this churning matter is revolving around the molten iron; but because of the fluidity, the molten iron does not participate in this rotation. The two compartments in the interior of the earth behave as if they were separate and thus, the arrangement completes the requirements to generate charge and the complimentary property of magnetism. It is noteworthy that in this hypothesis, the induced magnetism is in the outer layers of the planets and far away from the molten iron core and thus the heat in the inner core is not a hindrance. Since it is well-known that spin of even elementary particles generate charge (thus magnetism as well), it is not unreasonable to conclude that the same phenomenon applies to large bodies that spin rapidly, as well. By this argument one could predict that the planets that do not display magnetism are rotating very slowly; this is the case with Venus. It is unknown why Mars lacks magnetism but it may be that it lacks molten iron in the core. In the case of Mercury, the almost 85% of iron in its body and the proximity with the intensely magnetic neighbor, the Sun will adequately explain, despite the extremely slow axial rotation.
THE PURPOSE OF MAGNETISM IN PLANETS:
A question one has to answer with regards to magnetism is, why? Why do planets require magnetism? The role played by the magnetosphere surrounding the earth in protecting the planet from the harmful effects of the " solar winds" is well recognized. Since the magnetic axes roughly parallel the geologic axes, another reasonable explanation is as follows: the purpose of the magnetism is to help keep the bodies at appropriate distances from one another. How? This may be a function of repulsion of like-poles. Thus, the combined product of gravity and spin is aided by the magnetism to situate the bodies at appropriate distances, and in the same axial orientation. In bodies that do not display magnetism, the spin/gravity combination can still situate the planets and satellites at their appropriate locations; the magnetism has a complimentary function in this phenomenon. If this is true, this added effect of magnetism can help explain the inconsistency with the precession of the perihelion of the intensely magnetic body, the planet Mercury. One needs to remember also that Mercury is the closest neighbor of another highly magnetic body, the Sun. Finally, the appearance of the 'inversion' of the peripheral satellites of the gas giants needs an explanation. Obviously, the distance from the mother body has a major role in this, as attested to by the synchronous rotation in the nearby satellites and the 'normal' rotation of the satellites situated at intermediate distances from the mother. It is the small satellites located at the periphery, far away from the central body, which display this 'negative rotation'. One feature that can have this effect is a 'reversal' of the magnetic fluxes from the mother. Here one needs to speculate that the peripheral regions of the planet's sphere of influence display a reversal of the polarity and this flips the small peripheral satellites more or less upside down. This is testable, in future space missions.
HOW DOES SUN MOVE LARGE BODIES AROUND?
While it is not directly related to the central theme of this paper, it is useful to explore the question of how the very large bodies, the planets are hurtled by Sun (and, all satellites by their own mother bodies), from such vast distances. This is intriguing as gravity is but a feeble force. In order to understand this phenomenon, one has to free oneself from the earth-bound biases. As all bodies find themselves in only feeble gravitational pull from other bodies and the space is almost a vacuum (except the atmosphere in the immediate vicinity of the body), all bodies are essentially weight-less. Thus all bodies, however large, including all stars are as insignificant as fluff; thus the major body in their vicinity can move them along, with its gravitational pull, aided by the spin. To visualize this phenomenon at such large scales, one just needs a well-developed imagination.
SPIN IS THE MOST IMPORTANT FUNDAMENTAL PROPERTY OF MATTER
Classical physics teaching accepts the strong and weak nuclear forces, the gravity and electromagnetism as the four fundamental properties of matter. Although there have been suggestions of the spin also being fundamental to matter, no one has hitherto given it the importance it really has. The very fact that matter at the smallest and its grandest as well as bodies at their inception (such as the proto-stars) spin, signifies its fundamental status. Also, the Neutron stars' spinning abilities (the axial spin of some neutron stars exceed hundreds of times a second!) speak volumes about how fundamental this spin is, to bodies that exist free and when the conditions are right. Here, the neutron stars, which are the remnants of large stars after a supernova explosion, the electrons having departed and the neutrons and protons have fused together to form small spherical bodies, are behaving like the nucleus of the atoms. Even the very large luminous bodies in the center of all spiral galaxies are also spinning at incredible rates and, due to their enormous gravitational pull, they are able to carry the rest of the galaxies along, with the orderly spin. The currently accepted explanation of this phenomenon is the existence of "Super-massive Black Holes" in the center of the spiral galaxies (24). Current author proposes that, if the central luminous body is the result of collisions of billions of stars near the center of the galaxy, and thus behaving like a gigantic star (a sort of 'Galaxstar') such a body will have the power to move the whole galaxy around, by using the enormous gravity and the inherent spin. Equally important is the fact of the generation of electromagnetism due to the axial spin of the electrons (25). Therefore, of all the fundamental properties of matter, one could propose that the tendency to spin is the most important.
This paper offers explanations for some vexing problems in cosmology that scientists have been grappling with. In arriving at these proposals, a simple application of readily observed phenomena in the universe, such as axial spin and gravity, and magnetism is all that is required. By assigning the ubiquitous property of matter to spin on its own axis, its intended functions, we are able to explain the phenomena at the subatomic level as well as at the level of the planets, stars and galaxies, a unified theory of how matter behaves. The tendency of the scientific community to dismiss this property as simply a "conservation of the angular momentum" implying that it has no inherent purpose, is incorrect and a disservice.
I am deeply indebted to Ms. Rosie Gonzales for her excellent secretarial assistance and to Mr. Chamel Raghu for help with the figures. Sincere gratitude is also due to Dr. Lloyd Taylor for the many helpful suggestions, for providing statistical analysis of the data and for the construction of the figures.
1) E. Hubble, Proc. Natl. Acad. Sci. U.S.A 15, 168 (1929)
2) A.A. Penzias and R.W. Wilson, Astrophys. J. 142, 1149 (1965)
3) G.F. Smoot et al. Astrophys. J. 396, L1-L5 1992
4) A.H. Guth, Phys. Rev. D23:2, 347 (1981)
5) A.D. Linde, Phys. Lett B 389 (1982)
6) A. Albrecht. & P.J. Steinhardt, J. Phys. Rev. Lett. 48, 1220-1223 (1982)
7) S. Perlmutter et al. Astrophys.J. 517, 56 (1999)
8) A.G. Reiss et al. Astron. J. 116, 1009-1038 (1998)
9) R. P. Kirchner, Science 300, 1914 (2003)
10) P.J. E. Peebles, B. Ratra, Rev. Mod. Phys. Eng. Sci. 361, 2497 (2003)-
11) J. Bardeau, P.J. Steinhardt. P.J. & M.S. Turner, Phys. Rev. D28, 679-693, (1983)
12) A.A. Starobinskii, Lett. B117, 175-178 (1982)
13) S.W. Hawking, Phys. Lett. B115, 295-298 (1982)
14) E. Harrison, Phys. Rev. D1, 2726-2730 (1970)
15) A. Guth & P. Steinhardt, Scientific American, 116-18, May 1984
16) www.Spinninguniverse.com/articles/spinning_universe_a_hypothesis.html (last accessed date: April 18 2013
17) M.J. Longo, Physics Letters G, 699:4, 224 (2011)
18) P.K. Raghuprasad, in press, Physics Essays, 26:2, 331-338 June 2013
19) Dufton et al, Astrophys. J. Letters, 2011
20) B.A. Buffett, Science 288:5473, 2007-12 (2000)
21) G. Schubert, K. Zang et al, Nature 384, 544 (1996)
22) "Pierre Curie-Biography". Nobel Lectures, Physics 1901-21, Elsevier Publishing
Company, Amsterdam, 1967
23) Herndon, G.M., J. Geo-magnetism and Geo-electricity, 1993, 45: 423-437
24) Schodel, R. et al. Nature 419: 694-696, 2002
25) R.Elsberg, R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei and
Particles (2nd ed) pp 272-3
TABLE l
SELECTED PLANETARY FACT SHEET
|
|
Mercury |
Venus |
Earth |
Mars |
Jupiter |
Saturn |
Uranus |
Neptune |
Pluto |
|
Mass (1024Kg)
|
0.330
|
4.87 |
5.97 |
0.642 |
1,899 |
568 |
86.8 |
102 |
0.0125 |
|
Diameter (Km) |
4,879 |
12,104 |
12,756 |
6,792 |
142,984 |
120,536 |
57,118 |
49,528 |
2,390 |
|
Density (Kg/m3) |
5,427 |
5,243 |
5,515 |
3,933 |
1,326 |
687 |
1,270 |
1,638 |
1,750 |
|
Distance From sun (106Km) |
57.9 |
108.2 |
149.6
|
227.9 |
778.6 |
1,433.5 |
2,872.5 |
4,495.1 |
5,870 |
|
Orbital Velocity (km/sec) |
47.9 |
35 |
29.8 |
24.1 |
13.1 |
9.7 |
6.8 |
5.4 |
4.7 |
|
Orbital Period (days) |
88 |
224.7 |
365.2 |
687 |
4,331 |
10,747 |
30,589 |
59,800 |
90,588 |
|
Perihelion (106Km) |
46 |
107.5 |
147.1 |
206.6 |
740.5 |
1,352.6 |
2,741.3 |
4,444.5 |
4,435 |
|
Aphelion (106Km) |
69.8 |
108.9 |
152.1 |
249.2 |
816.6 |
1,514.5 |
3,003.6 |
4,545.7 |
7,304.3 |
|
Gravity (m/s2) |
3.7 |
8.9 |
9.8 |
3.7 |
23.1 |
9 |
8.7 |
11 |
0.6 |
|
Axial Tilt (Degrees) |
0.01 |
177.4 |
23.4 |
25.2 |
3.1 |
26.7 |
97.8 |
28.3 |
122.5 |
|
Rotation Period (h) |
1,407.6 |
*-5,832.5 |
23.9 |
24.6 |
9.9 |
10.7 |
*-17.2 |
16.1 |
*-153.3 |
*negative rotation = axial rotation opposite to that of the sun's
Adapted from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/index.html
ORBITAL VELOCITY DETERMINED BY REGRESSION
BASED ON DISTANCE FROM THE SUN AND ORBITAL VELOCITY
|
Planet |
Distance From Sun (106Km) |
Orbital Velocity (km/sec) |
|
Mercury |
57.9 |
47.9 |
|
Venus |
108.2 |
35 |
|
Earth |
149.6 |
29.8 |
|
Mars |
227.9 |
24.1 |
|
Jupiter |
778.6 |
13.1 |
|
Saturn |
1,433.50 |
9.7 |
|
Uranus |
2,872.50 |
6.8 |
|
Neptune |
4,495.10 |
5.4 |
|
Pluto |
5,870 |
4.7 |
ORBITAL PARAMETERS OF SATELLITES OF JUPITER*
|
Satellites: |
Radius (Km) |
Distance from Jupiter Δ (103Km) |
Orbital Period (Days) |
Rotation Period (Days) |
Inclination (Degrees) |
|
A) Galilean: |
|
|
|
|
|
|
Io |
1,821.6 |
421.6 |
1.769138 |
S |
0.04 |
|
Europa |
1,560.8 |
670.9 |
3.551181 |
S |
0.47 |
|
Ganymede |
2,631.2 |
1,070.4 |
7.154553 |
S |
0.21 |
|
Callisto |
2,410.3 |
1,882.7 |
16.689018 |
S |
0.51 |
|
B) ‘Lesser’ |
|
|
|
|
|
|
Metis |
20 |
128 |
0.294779 |
S |
0.06 |
|
Adrastea |
13x10x8 |
129 |
0.298260 |
S |
0.03 |
|
Amalthea |
131x73x67 |
181.4 |
0.498179 |
S |
0.40 |
|
Thebe |
55x45 |
221.9 |
0.6745 |
ND |
0.8 |
|
Themisto |
4 |
7,507 |
132.02 |
ND |
45.67 |
|
Leda |
5 |
11,170 |
240.92 |
ND |
27.47 |
|
Himalia |
85 |
11,460 |
250.5662 |
0.4 |
27.63 |
|
Lysithea |
12 |
11,720 |
259.22 |
ND |
27.35 |
|
Elara S/2000 J11 Carpo (S/2003 J20) |
40 2.0 3.0 |
11,740 12,560 16,990 |
259.6528 287.0 456.1 |
0.5 ND ND |
24.77 28.2 51.4 |
|
Euporie Orthosie Euanthe Thyone Mneme |
1 1 1.5 2 2.0 |
19,390 20,720 20,800 20,940 21,070 |
553.1 R 622.6 R 620.6 R 627.3 R 620.0 R |
ND ND ND ND ND |
147.0 145.9 148.9 148.5 148.6 |
|
Harpalyke Hermippe |
2.2 2 |
21,110 21,130 |
623.3 R 633.9 R |
ND ND |
148.7 150.7 |
|
Praxidike Thelxinoe Helike |
3.4 2.0 4.0 |
21,150 21,160 21,260 |
625.3 R 628.1 R 634.8 R |
ND ND ND |
148.7 151.4 154.8 |
|
Iocaste |
2.6 |
21,270 |
631.5 R |
ND |
159.7 |
|
Ananke Eurydome |
10 1.5 |
21,280 22,870 |
629.8 R 717.3 R |
ND ND |
148.9 150.3 |
|
Arche Autonoe Herse |
1.5 2 2.0 |
22,930 23,040 23,097 |
723.9 R 762.7 R 715.4 R |
ND ND ND |
165.0 152.9 164.2 |
|
Pasithee Chaldene |
1 1.9 |
23,100 23,180 |
716.3 R 723.8 R |
ND ND |
165.4 165.4 |
|
Kale |
1 |
23,220 |
729.5 R |
ND |
165.0 |
|
Isonoe Aitne |
1.9 1.5 |
23,220 23,230 |
725.5 R 730.2 R |
ND ND |
165.0 165.1 |
|
Erinome |
1.6 |
23,280 |
728.3 R |
ND |
164.9 |
|
Taygete |
2.5 |
23,360 |
732.2 R |
ND |
165.2 |
|
Carme Sponde |
15 1 |
23,400 23,490 |
734.2 R 748.3 R |
ND ND |
164.9 151 |
|
Kalyke |
2.6 |
23,580 |
743 R |
ND |
165.2 |
|
Pasiphae Eukelade |
18 4.0 |
23,620 23,660 |
743.6 R 746.4 R |
ND ND |
151.4 165.5 |
|
Megaclite Sinope Hegemono Aoede Kallichore |
2.7 14 3.0 4.0 2.0 |
23,810 23,940 23,950 23,980 24,040 |
752.8 R 758.9 R 739.6 R 761.5 R 764.7 R |
ND ND ND ND ND |
152.8 158.1 155.2 158.3 165.5 |
|
Callirrhoe |
4 |
24,100 |
758.8 R |
ND |
147.1 |
|
Cyllene Kore |
2.0 2.0 |
24,350 24,540 |
737.8 R 779.2 R |
ND ND |
149.3 152.4 |
C) Newly discovered satellites S/2000 J2 to S/2011 J2 have orbital periods from 504 to 982.5; all exhibit reverse 'motion'
and orbital inclination from 140.8 to 165
S=Synchronous rotation (rotation period is the same as orbital period) R=Retrograde rotation ND= No data available
Δ Distance from Jupiter (103km) = Semimajor Axis
*Adapted from:http://nssdc.gsfc.nasa.gov/planetary/factsheet/joviansatfact.html April 19, 2013
Reproduced with kind permission of Physics Essays Publication, http://physicsessays.org/ with modifications.
SYNCHRONOUS* ROTATION IN EARTH'S MOON AND THE
MAJOR SATELLITES OF THE GAS GIANTS^
|
Planet |
Satellites |
Diameter ( km) |
Distance from Mother Δ (103 km) |
Orbital Period (Hours) |
Rotation+ Period |
Orbital Velocity (km/sec) |
|
Earth |
Moon |
3,476.2 |
384 |
655.2 |
S
|
1.023 |
|
Jupiter |
Io Europa Ganymede Callisto
|
3643.2 3121.6 5262.4 4820.6 |
421.6 670.9 1070.4 1882.7 |
42.456 85.224 171.696 400.536 |
42.5 85.2 171.7 400.5 |
17.3 13.7 10.9 8.2
|
|
Saturn |
Mimas Enceladus Tethys Dione Rhea Titan Hyperion Iapetus
|
416x394x382 514x502x496 1076x1056x1052 1126x1122x1120 1530x1526x1524 5150 360x266x206 1492x1492x1424 |
185.52 238.02 294.66 377.40 527.04 1,221.83 1,481.1 3,561.3 |
22.618 32.885 45.307 65.686 108.42 382.69 510.638 1903.924 |
S S S S S S S S |
ND ND ND ND ND ND ND ND
|
|
Uranus |
Miranda Ariel Umbriel Titania Oberon
|
480x468.4x465.8 1162.2x1155.8x1155.4 1169.4 1577.8 1522.8 |
129.39 191.02 266.30 435.91 583.52 |
33.923 60.489 99.46 208.94 323.117 |
S S S S S |
ND ND ND ND ND
|
* Synchronous Rotation (S) = Rotation period is the same as the orbital period
^ Neptune's Satellites are not included as the details about the rotation are unavailable
Δ Distance from Mother = Semi-major Axis
+ Rotation period is available only for Jupiter's satellites. However, since all of the other satellites
listed in this table rotate "synchronously," for them the orbital period was used instead, in place of rotation period.
ND = No Data Available
*Adapted from: http://nssdc.gsfc.nasa.gov/planetary/factsheet
COMPARISON OF PLANETS WITH NEGATIVE ROTATION*
(VENUS, URANUS, AND PLUTO), TO EARTH AND JUPITER
|
|
Venus |
Uranus |
Pluto |
Earth |
Jupiter |
|
Mass (1024Kg) |
4.87 |
86.8 |
0.0125 |
5.97 |
1,899 |
|
Diameter (km) |
12,104 |
51,118 |
2,390 |
12,756 |
142,984 |
|
Rotation Period (hours) |
-5,832.5* |
-17.2* |
-153.3* |
23.9 |
9.9 |
|
Length of Day (hrs) |
2,802 |
17.2 |
153.3 |
24 |
9.9 |
|
Orbital Inclination (Degrees) |
3.4 |
0.8 |
17.2 |
0.0 |
1.3 |
|
Axial Tilt (Degrees) |
177.4 |
97.8 |
122.5 |
23.4 |
3.1 |
|
Magnetic Field |
No |
Yes |
Unknown |
Yes |
Yes |
*Negative rotation means axial rotation opposite to that of the Sun
Adapted from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/index.html
Reproduced with kind permission of Physics Essays Publication, http://physicsessays.org/